Search

Integral: Sifat, Rumus, Jenis & Contoh Soal dengan Jawabannya

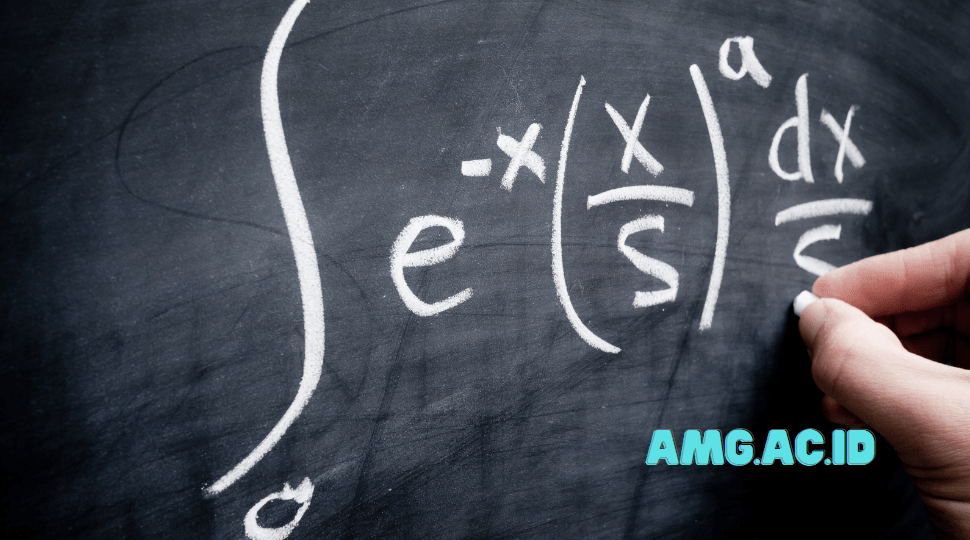
Matematika adalah subjek yang menarik dan penting dalam kehidupan sehari-hari. Salah satu konsep utama dalam matematika adalah integral. Dalam artikel ini, kami akan membahas integral mulai dari konsep dasar hingga contoh soal dengan jawabannya yang mudah dimengerti oleh anak-anak sesuai dengan kurikulum terbaru. Dalam proses pembelajaran, penting untuk menciptakan lingkungan yang menyenangkan dan memotivasi anak-anak untuk belajar matematika dengan antusiasme.

Apa Itu Integral & Perannya Dalam Matematika ?

Integral dalam matematika merujuk pada salah satu konsep utama dalam kalkulus. Integral digunakan untuk menghitung luas daerah di bawah kurva fungsi, serta memiliki berbagai aplikasi lainnya seperti menghitung volume, menghitung rata-rata, menyelesaikan persamaan diferensial, dan banyak lagi.

Secara sederhana, integral dapat dianggap sebagai operasi yang berlawanan dengan diferensiasi. Jika diferensiasi adalah proses untuk mencari turunan fungsi, maka integral adalah proses untuk mencari fungsi asal (primitif) dari turunan fungsi tersebut.

Integral memiliki peran yang sangat penting dalam matematika. Berikut adalah beberapa alasan mengapa integral penting dalam bidang ini:

Menghitung Luas dan Volume: Integral memungkinkan kita untuk menghitung luas daerah di bawah kurva fungsi. Dalam dimensi yang lebih tinggi, integral juga digunakan untuk menghitung volume benda-benda ruang.

Menganalisis Perubahan: Integral digunakan untuk menganalisis perubahan dalam berbagai konteks, seperti perubahan jumlah, kecepatan, dan percepatan. Konsep integral memungkinkan kita untuk memahami perubahan secara mendalam.

Memprediksi dan Memodelkan: Integral digunakan dalam pembuatan model matematika yang memungkinkan kita untuk memprediksi fenomena alam, menganalisis perilaku sistem dinamis, dan memecahkan berbagai masalah nyata.

Penerapan dalam Fisika dan Rekayasa: Integral adalah alat penting dalam pemodelan dan analisis dalam bidang fisika dan rekayasa. Dalam mekanika, hukum-hukum gerak Newton dapat dirumuskan dengan menggunakan integral.

Pemahaman Konsep Dasar Matematika: Integral membantu dalam memahami konsep-konsep dasar matematika seperti luas, volume, kecepatan rata-rata, probabilitas, dan banyak lagi. Konsep ini kemudian menjadi dasar bagi pengembangan konsep yang lebih lanjut dalam matematika.

Ilustrasi konsep integral dengan contoh grafik fungsi

Untuk memberikan ilustrasi konsep integral, mari kita gunakan contoh grafik fungsi sederhana y = f(x). Dalam ilustrasi ini, kita akan memperlihatkan bagaimana integral dapat digunakan untuk menghitung luas daerah di bawah kurva fungsi tersebut.

Misalkan kita memiliki fungsi sederhana y = x^2 yang akan kita integralkan dalam rentang tertentu. Berikut adalah contoh grafik fungsi tersebut:

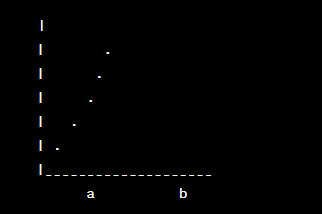
Pada grafik di atas, garis lengkung menggambarkan kurva fungsi y = x^2. Misalkan kita tertarik untuk menghitung luas daerah di antara kurva fungsi ini dan sumbu x pada rentang antara a dan b.

Langkah pertama adalah membagi daerah tersebut menjadi segmen-segmen yang lebih kecil. Semakin banyak segmen yang digunakan, semakin akurat hasil integralnya. Mari kita bagi daerah tersebut menjadi beberapa segmen persegi panjang yang terletak di bawah kurva, seperti ini:

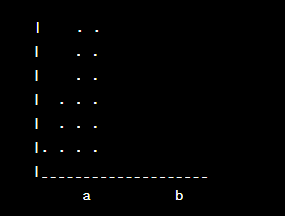
Kita dapat melihat bahwa setiap segmen persegi panjang memiliki lebar yang sama, tetapi tingginya berubah-ubah sesuai dengan nilai fungsi pada titik-titik yang dipilih. Dalam hal ini, tinggi setiap segmen adalah f(x) dan lebarnya adalah Δx.

Kita dapat mengekspresikan luas setiap segmen sebagai luas persegi panjang, yaitu panjang sisi pendek (Δx) dikalikan dengan tinggi (f(x)). Jika kita menambahkan luas semua segmen ini, kita akan mendapatkan perkiraan luas daerah di bawah kurva fungsi, yaitu:

Luas ≈ Σ [f(x) * Δx]

Namun, agar perkiraan tersebut semakin akurat, kita perlu menggunakan jumlah segmen yang lebih banyak dan memperkecil lebar setiap segmen (mendekati nol). Dalam limit yang tak hingga, jumlah segmen mendekati tak terhingga dan lebar setiap segmen mendekati nol, yang dituliskan dalam notasi integral:

Luas = ∫[f(x) dx]

Dalam contoh ini, kita akan mencari luas daerah di bawah kurva fungsi y = x^2 pada rentang antara a dan b. Dengan melakukan proses integral, kita akan mendapatkan nilai pasti luas daerah tersebut.

Ilustrasi ini menggambarkan cara kerja dasar integral dalam menghitung luas di bawah kurva fungsi. Metode ini dapat diterapkan pada berbagai fungsi matematika dan rentang yang berbeda. Integral memungkinkan kita untuk menggambarkan hubungan antara fungsi dan luas di bawahnya, dan memberikan alat yang kuat untuk menganalisis dan memodelkan berbagai fenomena matematika dan fisika.

Membaca notasi integral dan mengenali variabel-variabelnya

Notasi integral dalam matematika biasanya ditulis menggunakan simbol “∫” dan menyertakan fungsi yang akan diintegralkan di dalam kurung. Di luar kurung, terdapat variabel yang menunjukkan variabel integrasi yang digunakan dalam proses integral. Berikut adalah cara membaca notasi integral dan mengenali variabel-variabel yang terlibat:

1. Simbol Integral (∫)
   Simbol integral (∫) merupakan simbol khusus yang digunakan untuk menunjukkan operasi integral. Simbol ini menunjukkan bahwa kita sedang melakukan proses integral terhadap suatu fungsi.
2. Fungsi yang Diintegralkan
   Fungsi yang akan diintegralkan ditulis di dalam kurung (∫). Fungsi ini merupakan fungsi yang ingin kita hitung integralnya. Misalnya, jika kita memiliki fungsi f(x), maka notasi integral akan terlihat seperti ini: ∫f(x)dx. Fungsi ini akan menjadi “f(x)” yang kita integralkan.
3. Variabel Integrasi
   Variabel yang terletak di luar kurung (∫) adalah variabel integrasi. Variabel ini menunjukkan variabel yang digunakan dalam proses integrasi. Variabel ini ditulis setelah “dx” yang berarti “differential x” dan menunjukkan bahwa kita sedang melakukan integrasi terhadap variabel x. Namun, kita juga dapat menggunakan variabel lain seperti “dt”, “dy”, atau variabel lainnya tergantung pada konteks yang diberikan.

Sebagai contoh, jika kita ingin mengintegrasikan fungsi f(x) terhadap variabel x, maka notasi integral akan terlihat seperti ini: ∫f(x)dx. Bacalah notasi ini sebagai “integral dari f(x) terhadap x”. Artinya, kita sedang mencari integral dari fungsi f(x) terhadap variabel x.

Selain variabel integrasi, terkadang kita juga menggunakan batas-batas integrasi pada notasi integral. Batas-batas integrasi menentukan rentang di mana integral dilakukan. Batas atas dan batas bawah dituliskan di atas dan di bawah simbol integral, misalnya: ∫[a, b] f(x) dx. Bacalah notasi ini sebagai “integral dari a hingga b dari f(x) terhadap x”. Artinya, kita sedang mencari integral dari fungsi f(x) terhadap variabel x dalam rentang dari a hingga b.

Pemahaman tentang notasi integral dan variabel-variabel yang terlibat sangat penting dalam memahami dan menerapkan konsep integral dalam matematika. Dengan membaca notasi dengan benar, kita dapat mengidentifikasi fungsi yang diintegralkan, variabel integrasi yang digunakan, dan batas-batas integrasi yang terlibat dalam proses integral.

Jenis-Jenis Integral dan Contoh Soal Beserta Penjelasan

Integral Tak Tentu

Integral tak tentu adalah jenis integral yang mencari primitif atau fungsi asal dari suatu fungsi. Dalam notasi integral, integral tak tentu dituliskan sebagai ∫f(x)dx, di mana f(x) adalah fungsi yang akan diintegralkan dan dx adalah variabel integrasi.

Contoh Soal:

Hitunglah integral tak tentu dari fungsi f(x) = 3x^2 + 2x – 1.

Penyelesaian:

Dalam kasus ini, kita ingin mencari primitif dari fungsi f(x). Kita dapat menggunakan aturan integral untuk masing-masing suku fungsi ini. Berikut adalah penyelesaiannya:
∫(3x^2 + 2x – 1)dx = x^3 + x^2 – x + C,
di mana C adalah konstanta integrasi.

Integral Tentu

Integral tentu adalah jenis integral yang menghitung luas di bawah kurva fungsi dalam interval tertentu. Dalam notasi integral tentu, integral dituliskan sebagai ∫[a, b]f(x)dx, di mana [a, b] adalah interval di mana integral dilakukan.

Contoh Soal:

Hitunglah integral tentu dari fungsi f(x) = 2x di interval [0, 3].

Penyelesaian:

Kita ingin menghitung luas di bawah kurva fungsi f(x) = 2x dalam interval [0, 3]. Dalam kasus ini, kita dapat menghitung integral tentu dengan menggunakan rumus integral untuk fungsi linier:
∫[0, 3]2xdx = [x^2]0^3 = 3^2 – 0^2 = 9.

Jadi, integral tentu dari fungsi f(x) = 2x dalam interval [0, 3] adalah 9.

Integral Substitusi

Integral substitusi adalah metode yang digunakan untuk mengganti variabel dalam integral dengan variabel baru. Tujuan dari metode ini adalah untuk menyederhanakan integral dan membuatnya lebih mudah untuk dihitung. Dalam integral substitusi, variabel baru dipilih sehingga akan menghasilkan diferensial baru yang lebih sederhana dalam integral.

Contoh Soal:

Hitunglah integral ∫(2x + 1)^3 dx menggunakan metode integral substitusi.

Penyelesaian:

1. Langkah pertama dalam integral substitusi adalah memilih variabel baru yang akan menggantikan variabel dalam integral. Kita akan memilih variabel baru u = 2x + 1. Dalam kasus ini, u berperan sebagai variabel baru.
2. Selanjutnya, kita perlu menghitung diferensial variabel baru tersebut. Dalam hal ini, kita dapat menggunakan aturan diferensial untuk variabel u. Dalam kasus ini, du/dx = 2, sehingga du = 2dx.
3. Kita kemudian mengganti variabel dalam integral dengan variabel baru yang telah kita pilih. Dalam kasus ini, kita mengganti 2x + 1 dengan u:
   ∫(2x + 1)^3 dx = ∫u^3 * (du/2).
4. Setelah mengganti variabel, kita dapat menyederhanakan integral menjadi bentuk yang lebih sederhana. Dalam kasus ini, kita membagi integral dengan 2 sehingga menjadi:
   (1/2) ∫u^3 du.
5. Sekarang, kita dapat menghitung integral dari u^3 dengan menggunakan aturan integral untuk suku-suku polinomial. Dalam kasus ini, integral dari u^3 adalah (1/4)u^4.
6. Terakhir, kita memasukkan kembali variabel asli ke dalam hasil integral. Dalam kasus ini, variabel asli adalah x. Oleh karena itu, hasil akhir integral substitusi adalah:
   (1/2) * (1/4) * (2x + 1)^4 + C,
   di mana C adalah konstanta integrasi.

Jadi, integral dari (2x + 1)^3 menggunakan metode integral substitusi adalah (1/8) * (2x + 1)^4 + C.

Metode integral substitusi sangat berguna ketika kita menghadapi integral yang kompleks atau sulit dipecahkan secara langsung. Dengan memilih variabel baru yang tepat, kita dapat menyederhanakan integral dan mempermudah proses perhitungannya. Penting untuk memahami konsep integral substitusi dan menguasai tekniknya karena ini merupakan salah satu metode yang umum digunakan dalam kalkulus.

Integral Parsial

Integral parsial adalah metode yang digunakan untuk menghitung integral dari perkalian dua fungsi yang kompleks dengan menggunakan aturan turunan produk (peraturan Leibniz). Metode ini berguna ketika menghadapi integral yang sulit atau rumit yang tidak dapat dipecahkan dengan metode integral substitusi atau metode lainnya.

Contoh Soal:

Hitunglah integral ∫x sin(x) dx menggunakan metode integral parsial.

Penyelesaian:

1. Langkah pertama dalam integral parsial adalah memilih dua fungsi yang akan dikalikan. Dalam kasus ini, kita memilih x dan sin(x).
2. Selanjutnya, kita perlu menghitung turunan dari fungsi pertama (x) dan integral dari fungsi kedua (sin(x)). Turunan dari x adalah 1, sedangkan integral dari sin(x) adalah -cos(x).
3. Setelah menghitung turunan dan integral, kita menggunakan aturan turunan produk (peraturan Leibniz) yang menyatakan bahwa ∫(u v’) dx = u v – ∫(u’ v) dx.
4. Dalam kasus ini, kita memiliki:
   ∫x sin(x) dx = -x cos(x) – ∫(-cos(x) * 1) dx.
5. Sekarang, kita dapat menyederhanakan integral yang tersisa. Dalam kasus ini, integral dari -cos(x) * 1 adalah ∫cos(x) dx = sin(x).
6. Terakhir, kita mendapatkan hasil akhir integral dengan menggabungkan hasil substitusi sebelumnya:
   ∫x sin(x) dx = -x cos(x) – (-sin(x)) + C,
   di mana C adalah konstanta integrasi.

Jadi, integral dari x sin(x) menggunakan metode integral parsial adalah -x cos(x) + sin(x) + C.

Integral Trigonometri

Integral trigonometri adalah jenis integral yang melibatkan fungsi trigonometri, seperti sin(x), cos(x), tan(x), dan sejenisnya. Integral trigonometri sering digunakan dalam pemecahan masalah yang melibatkan siklus periodik, seperti perhitungan luas di bawah kurva trigonometri atau perhitungan torsi dalam fisika.

Contoh Soal:

Hitunglah integral ∫tan(x) dx menggunakan integral trigonometri.

Penyelesaian:

1. Dalam kasus ini, kita ingin menghitung integral dari tan(x). Integral dari tan(x) tidak dapat dihitung langsung menggunakan aturan integral trigonometri karena tidak memiliki bentuk yang sederhana seperti integral dari sin(x) atau cos(x).
2. Namun, kita dapat menggunakan metode substitusi untuk mengatasi integral ini. Misalkan kita mengganti tan(x) dengan sin(x)/cos(x). Dalam hal ini, kita mengganti tan(x) dengan sin(x)/cos(x) dalam integral.
3. Setelah mengganti tan(x), kita dapat membagi integral menjadi dua integral yang lebih sederhana:
   ∫tan(x) dx = ∫(sin(x)/cos(x)) dx.
4. Integral tersebut dapat diselesaikan menggunakan metode integral substitusi dengan memilih u = cos(x). Setelah menghitung diferensialnya, du = -sin(x) dx.
5. Dengan mengganti sin(x) dx dengan -du dalam integral, kita mendapatkan:
   ∫tan(x) dx = -∫(1/u) du = -ln|u| + C,
   di mana ln|u| adalah fungsi logaritma natural dari |u| dan C adalah konstanta integrasi.
6. Terakhir, kita kembali menggunakan variabel asli (x) dalam hasil integral:
   ∫tan(x) dx = -ln|cos(x)| + C.

Jadi, integral dari tan(x) menggunakan integral trigonometri adalah -ln|cos(x)| + C.

Kesimpulan

Dalam artikel ini, kita telah menjelajahi konsep integral, jenis serta contohnya dengan tujuan memberikan pemahaman yang mudah dimengerti bagi anak-anak sesuai dengan kurikulum terbaru. Integral merupakan salah satu konsep penting dalam matematika yang digunakan untuk menghitung luas daerah di bawah kurva fungsi, memodelkan perubahan, dan menganalisis berbagai fenomena matematika dan fisika.

Pemahaman tentang konsep integral adalah kunci penting dalam pengembangan keterampilan matematika. Dengan memanfaatkan pendekatan yang mudah dimengerti dan menyenangkan, anda dapat menguasai konsep integral dengan baik, memperluas wawasan matematika mereka, dan membuka pintu untuk pemecahan masalah yang lebih kompleks di masa depan.

Related Post to Integral: Sifat, Rumus, Jenis & Contoh Soal dengan Jawabannya